Drawing lines on a computer.
The other day, I was searching for a minimalist library to draw simple shapes in Rust. Then, I thought that I had never really dove into low-level details of graphics rendering. Caution here, what I mean by low level here is not hardware or driver. Upon online researches, I concluded that there is an tremendously big iceberg of abstraction for rendering pixels on a screen.
To start simple, I decided to render simple lines strokes to the lowest level I was interested in. That is to say defining the shape at the vertex level and using OpenGL shaders for GPU rendering.
This post describes the several steps I followed.
1. A bit of theory
Before talking about lines, let's talk about shapes in general.
1.1 Shapes
The vast majority of what is drawn on your computer screen, be it lines or squares, are actually defined as collections of triangles.

The triangle is the fundamental primitive / building block of graphics rendering. Of course, there are some approximations used along the way to render other things, such as circles or cats. For example, it is not possible to draw a perfect circle using only triangles: but with sufficiently enough of them, you could create a really good illusion.
1.2 Lines strokes
A line with a constant thickness can be built from triangles. There are probably various methods out there, I will expose the one I came with.
1.3 Points and edges
First, we define a collection of $n$ points $\mathcal{P}:{p_0, p_1, ..., p_{n-1}}$ on which the line should be centered. This is the skeleton of the line stroke.

Then, we need to add thickness. The first idea is to construct another line slighly above and fill the shape. But it's fairly obvious that a simple translation of $\mathcal{P}$ points would fail.
Where should the points of this second line go ?
The answers lies in using the normals of the edges between points of $\mathcal{P}$. A normal is a vector that is orthogonal to another, which also implied that their scalar product is zero.
Let's note $\mathcal{E}$ the set of edges between each points in $\mathcal{P}$. $\mathcal{E}$ contains $n-1$ edges.

1.4 Edge normal vectors
For each edge $\vec{e_i}=[x, y]$, we can compute a normal vector $\vec{e_i}=[-y, x]$ or $[y, -x]$.
e.g. If $\vec{e_i}=[1, 2]$, one normal vector could be $\vec{n_i}=[-2, 1]$, indeed $\vec{e_i} \cdot \vec{n_i}=0$.
Also note that from now, I will only work with normalized (normal) vectors, that is to say of norm $1$.
Edge normals are one part of the story, but not the end. What we need next is a normal vector for each point, or vertex. See, what we are actually aiming for is something that looks likes this (with slight modifications we will see after) :

We somehow need to find out the direction of extrusion for each point or vertex.
1.5 Vertex normal vectors
For the first and last vertices, the vertex normal is simply the respective edge normal, since there is no other point before and after.
For all other points however, the direction in which the strokes expands depends actually on both sides. The direction we are aiming for is this one:

This is the bissector of $\vec{n_1}$ and $\vec{n_2}$, which we give a little name : $\vec{b_1}$.
We can find this actual vector by taking the sum of $\vec{n_1}$ and $\vec{n_2}$ and normalizing.
$$ \vec{b_i}=\frac{\vec{n_i}+\vec{n_{i+1}}}{\lVert \vec{n_i}+\vec{n_{i+1}} \rVert} $$
Again, this is not the end of the story, $\vec{b_i}$ is only the direction we shall go towards to extrude the point, but we do not yet how by how much.
1.6 Finding the new points
We are nearly ready to draw the lines strokes. While we are at it, let's notate our stroke width $u$.
To define the new points that will be used to draw the overall filled shape, we can follow theses steps:
- For each point $p$ in $\mathcal{P}$.
- Compute the vertex normal $\vec{b}$ of $p$.
- Add the vertex normal $\vec{b}$ times $u$ to $p$ to obtain new $\hat{p}$.
This seems logical, but it's wrong. This would make a sensible shape, but not of constant width.
See, if there is a slight angle between two adjacent edges (and it will, if we are not drawing only straight lines), adding $u$ times $\vec{b}$ will make the distance between $p$ and $\hat{p}$ equal to $u$ in the $\vec{b}$ direction, but not elsewhere. What we want is actually the opposite.

The triangle at the top illustrates fully the issue. We want the bottom side to be of length $u$, not the hypothenuse. So how should be set the length $k$ of the hypothenuse (the amount of displacement really) so that the adjacent has a length $u$ ? Well, the projection of $k\cdot \vec{b}$ on $\vec{n_0}$ should be equal to $u$, that is to say:
$$ k\cdot \vec{b} \cdot \vec{n_0} = u $$ Then,
$$ k = \frac{u}{ \vec{b} \cdot \vec{n_0}} $$
This is the actual factor we should use. Using this version, the steps to draw our new points are:
- For each point $p$ in $\mathcal{P}$.
- Compute the vertex normal $\vec{b}$ of $p$.
- Add the vertex normal $\vec{b}$ times $k$ to $p$ to obtain new $\hat{p}$.
1.7 The triangles
Now that all the vertices are now defined, how should be triangulate everything ? One solution is to observe that each that $p_i$, $p_{i+1}$, $\hat{p_i}$ and $\hat{p}_{i+1}$ form a quad, which we can split in two triangles, like so:
1.8 Theory wrap up
This is the main idea, now the practice involves implementing this algorithm in a language that actual computers can understand.
2. Pratice
I decided to implement the graphics rendering using Rust and a light wrapper around OpenGL called glium. The crate handles the nasty OpenGL parts to give you quick access to a window handles and buffer as well GL shaders.
2.1 Algorithm implementation
First, let's implement what we described just before. We need a function that computes the vertex normals. This takes as input a vector of 2D points and outputs a vector (data structure) of 2D vectors (geometry).
fn compute_vertex_normals(points: &mut Vec<Point2>) -> Vec<Vec2> {
...
}
Edges normals are the first to be computed, using iterators on adjacent points:
let mut segment_normals = vec![];
for (p0, p1) in zip(points.iter(), points.iter().skip(1)) {
let segment = p1.sub(*p0);
let normal = vec2(-segment.y, segment.x).normalize();
segment_normals.push(normal);
}
By the way, it is not probably the best way to express this loop, but coming from Python, I like the elegance of:
for element, next_element in zip(vec, vec[1::])
Then, the normals of vertices can be computed:
// Compute normals of vertices
let mut vertex_normals = vec![];
for (s_normal_prev, s_normal_next) in zip(
edge_normals.iter(), edge_normals.iter().skip(1)) {
vertex_normals.push(s_normal_prev.add(*s_normal_next).normalize());
}
vertex_normals.insert(0, *edge_normals.first().unwrap());
vertex_normals.push(*edge_normals.last().unwrap());
We iterate on the adjacent edge normals and compute the vertex normals, not forgetting to add the first and last vertex normals as the two ends edge normals.
Last, we build the triangles:
// Iterators on points and vertices normals
let zip_points = zip(points.iter(), points.iter().skip(1));
let zip_vertex_normals = zip(vertex_normals.iter(), vertex_normals.iter().skip(1));
// Build triangles
for ((p0, p1), (n0, n1)) in zip(zip_points, zip_vertex_normals) {
let u = WIDTH;
let edge = p1.sub(*p0);
let normal = vec2(-edge.y, edge.x).normalize();
let k0 = u / n0.dot(normal);
let k1 = u / n1.dot(normal);
let tri0: (Point2, Point2, Point2) = (
p0.sub(*n0 * k0 / 2.0),
p0.add(*n0 * k0 / 2.0),
p1.add(*n1 * k1 / 2.0),
);
let tri1: (Point2, Point2, Point2) = (
p0.sub(*n0 * k0 / 2.0),
p1.add(*n1 * k1 / 2.0),
p1.sub(*n1 * k1 / 2.0),
);
tris.push(tri0);
tris.push(tri1);
}
Iterating of the points and normals, I build two different triangles each time and push it into a vector a triangles (tuples of 2D points).
I did something a bit different here. Because I wanted the stroke to be centered on the line made by the points, I'm actually moving the points upwards and downwards along the normal, instead of just upwards (that's why the /2.0 are everywhere). This doesn't change the philosophy, it's simply prettier as a result.
2.2 Vertex buffer
Once our triangle are computed on the CPU, it is now the time to send them to the GPU for rendering.
First, we have to actually convert my 2D points to Vertex structure that are understood by OpenGL. My vertices will have two attributes:
#[derive(Copy, Clone)]
struct Vertex {
position: [f32; 2],
color: [f32; 4],
}
implement_vertex!(Vertex, position, color);
Then, we iterate on the vertices of the triangles, and create a new vertex with a color :
for (index, tri) in tris.iter().enumerate() {
let (tri0, tri1, tri2) = tri;
vertices[index * 3] = Vertex {
position: [tri0.x, tri0.y],
color: [0.0, 0.0, 1.0, 1.0],
};
vertices[index * 3 + 1] = Vertex {
position: [tri1.x, tri1.y],
color: [0.0, 1.0, 0.0, 1.0],
};
vertices[index * 3 + 2] = Vertex {
position: [tri2.x, tri2.y],
color: [1.0, 0.0, 0.0, 1.0],
}
}
Those who are following will see that some vertices will be declared 2 times, and that's true. This is not optimal as we could (should?) reuse existing vertices and use well chosen indices to define our triangles in order to reduce the size of the vertex buffer passed to the GPU. For our example, this will work. Just keep in mind that's it's a crude way that could work faster.
2.3 Vertex shader
Then we tackle shaders. The first one I will be using is the vertex shader, that simply set the position of vertices according to the position attribute of my Vertex structure. I also pass on the color attribute to next stages of rendering pipeline.
#version 140
in vec2 position;
in vec4 color;
out vec4 o_color;
void main() {
gl_Position = vec4(position, 0.0, 1.0);
o_color = color;
}
2.4 Fragment shader
The fragment shader simply assign my color attribute to the fragment and is responsible for displaying the beautiful color interpolation you'll see just after.
#version 140
in vec4 o_color;
out vec4 color;
void main() {
color = o_color;
}
2.5 Sending the program to the GPU
It is now time to generate a bunch of points, compute triangles and vertices, and send them to OpenGL in order to admire our results.
let vertex_buffer = { glium::VertexBuffer::new(&display, &vertices).unwrap() };
let program = glium::Program::from_source(
&display,
vertex_shader_src,
fragment_shader_src,
None,
)
We first create a buffer containing all of our vertices, and define an OpenGL program with our vertex and fragment shaders.
We can then ask for a draw and see the result.
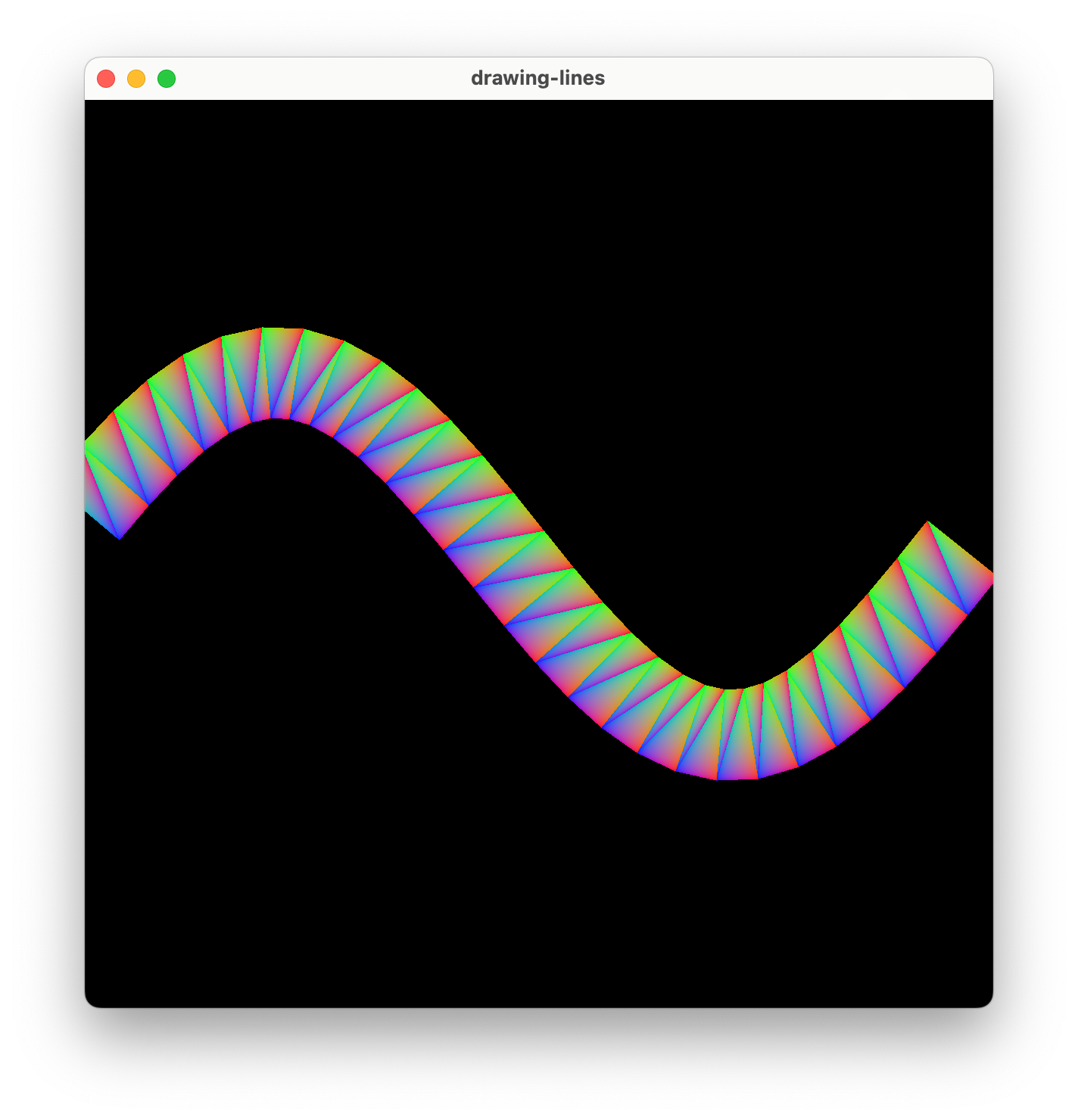
In order to get a little more interesting output, let's add a bit of movement on a 3:5 Lissajou's curve!
2.6 Improvements
Actually, the whole geometry could be computed in the vertex shader instead of from the CPU. We would have to send the displacement along the vertex position, and the geometry computation would occur on the GPU.
Also, as I already mentioned, a better use of indices could reduce the number of vertices passed into the vertex buffer.
3. Conclusion
I hope you liked this little walkthrough. Even simple things, drawing a line, can go a long way theses days.
